퍼셉트론

'밑바닥부터 시작하는 딥러닝' 이라는 책을 참고하여 작성하였습니다.

 

 

퍼셉트론은 다수의 신호를 입력받아서 하나의 신호를 출력하는 것

 

입력이 2개인 퍼셉트론을 보도록 하자

x는 입력값, w는 가중치, b는 편향이라고 할 때

 

y = x1*w1 + x2*w2 + b

 

y의 값이 1을 넘으면 1을 출력.

못넘으면 0을 출력

 

편향과 가중치는 다르다.

가중치는 각 입력 신호가 결과에 영향력을 조절하는 매개변수이고

편향은 뉴련이 얼마나 쉽게 활성화되는지 결정한다.

 

 

---

 

<구현>

논리게이트 AND, NAND, OR, XOR를 구현해보도록 하자.

 

import numpy as np
import matplotlib.pyplot as plt

def AND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.7
    tmp = np.sum(x*w) + b
    if tmp <= 0:
        return 0
    else:
        return 1

def NAND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([-0.5, -0.5])
    b = 0.7
    tmp = np.sum(x*w) + b
    if(tmp <= 0):
        return 0
    else:
        return 1

def OR(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.2
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

def XOR(x1, x2):
    return AND(NAND(x1, x2), OR(x1, x2))

m = [[0, 0], [0, 1], [1, 0], [1, 1]]

for i in range(len(m)):
    print(m[i][0], m[i][1])

for i in range(len(m)):
    print(XOR(m[i][0], m[i][1]))

가중치와 임계치의 조절만으로 여러 게이트를 구현하는 것을 볼 수가 있다.

 

 

 

 

XOR게이트에서 (0, 1), (1, 0)은 1이고 (0, 0), (1, 1)은 0이다.

전자의 영역을 동그라미로 표현하고 후자를 세모로 표현해서 그래프로 보자.

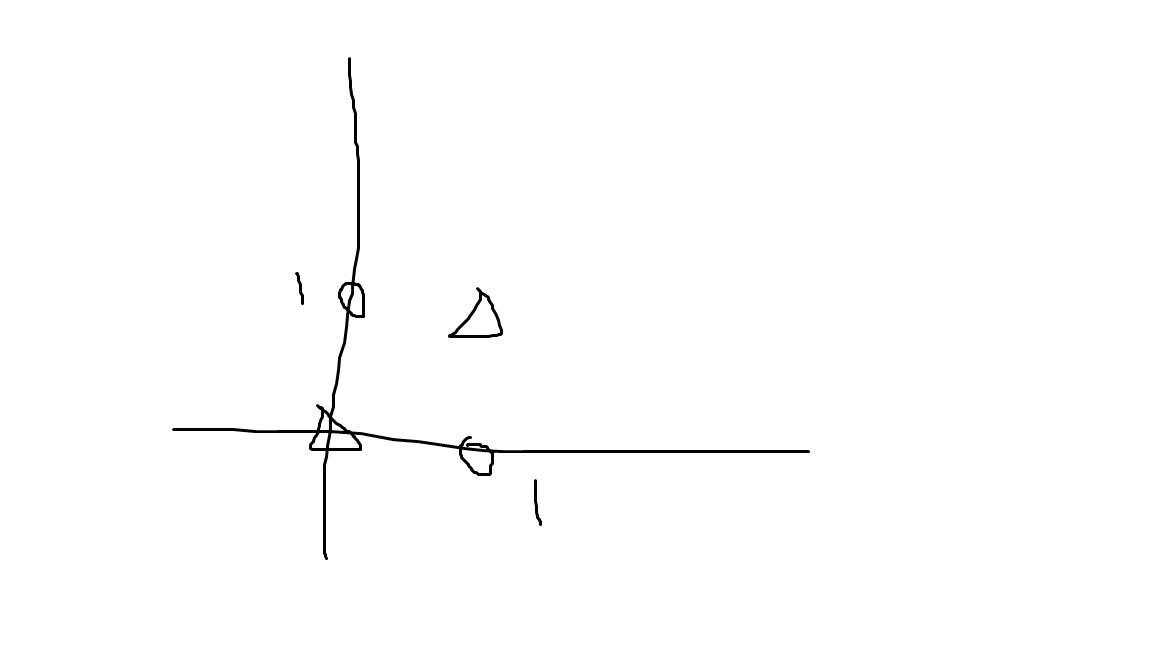
XOR게이트 값 표현

같은 모양은 같은 영역안에 있어야한다.

하지만 단층 퍼셉트론은 선형 영역을 갖기때문에 위의 값을 나눌 수가 없다.

이것이 단층 퍼셉트론의 한계다.

그래서 XOR는 다층 퍼셉트론으로 구현되었다.